动力集中动车组单线隧道内列尾流固耦合振动研究-和记娱乐怡情博娱188

“复兴号”cr200j动力集中型动车组自2019年运行以来，列车尾部在单线隧道内车体持续的大幅度横向晃动以致司乘人员难以接受，引起了主机厂、运营单位和科研院所的高度重视。在2020年6月由铁科院组织的时速160公里动力集中型动车组在西安局管内进行的试验发现，当列车通过单线隧道时出现了列车尾部明显的周期性晃车现象，振动主频范围在1–2hz，动力车司机室横向平稳性指标达到3.4，加速度达到2.4m/s2，由此判断该晃车现象是由隧道内列车尾部气流扰动引起。到目前为止，国内外时速160公里等级及以下的机车出现1hz左右的车体横向低频晃动现象公开发表可供借鉴的研究论文较少。而对于隧道内动车组列尾的异常晃车现象，则主要因隧道内列车与周围流场相互作用引起，需要从车辆系统动力学与空气动力学联合仿真角度来研究。

 

气流涡激振动在大跨度桥梁和深海采油立管流致振动等领域有着深入的研究，形成了系统的研究体系。流体经过钝形截面结构时因旋涡脱落出现交替变化作用力导致结构在来流方向和垂直方向振动，而结构振动又会改变其尾流结构，加剧流体作用，这种流体与结构相互作用被称为涡激振动，当涡激力与结构固有振动频率接近时引起共振称为涡激共振。同样，高速运行的列车尾部气流会出现周期性的漩涡脱落现象，对列车车体形成周期性的激励，该涡激力的频率主要取决于列车运行速度和车头结构形状。

 

高速列车的尾流是非常复杂的湍流流动，具有很高的湍流强度。通常来说，高速列车尾流是一个包含剪切层、卡门涡街类似的涡脱落、分离和再附着区以及一对旋向相反流向涡组成的非定常流动。在列车侧面会发生类似卡门涡街的脱落涡，同时这些涡相互融合和干涉，进而在时变的尾流中形成周期性展向振荡的一对涡旋，对气动问题发挥着重要的影响作用[6]。田红旗[7]研究表明漩涡主要源于复杂突变以及曲率大的表面，列车底部（转向架）、列车尾部以及尾流区域漩涡分布密集，正由于列车底部大量漩涡的存在严重影响列车的蛇行运动稳定性。指出尾车部位由于存在涡旋的生成和脱落等，对压差阻力的贡献明显，而针对头型的优化设计具有较好减阻效果。此外，高速列车运行的稳定性往往与气动特性关系密切，其中与尾涡相关的气动力是不容忽视的。列车车体的显著特点是大长细比（长细比，即列车长度与高度的比值），因此，车身表面的边界层要厚得多，从而分离剪切层也会很厚。高速列车尾车头部形状类似于morel试验研究中的几何模型，由于头型截面的变化，导致车身表面湍流边界层的流动分离以及流向的螺旋流动。baker认为这些现象是尾涡结构产生机理的构成要素，尾涡结构的最主要特征是成对且反向旋转的流向涡旋。研究发现，流向涡对当向下游传播时，由于彼此之间的诱导以及与地面之间的相互作用，会向下（垂向）以及向外侧（展向)进行移动，该现象与“common-flowdown”型涡对相似。并且，尾涡结构表现出展向振荡，类似于卡门涡街的周期性脱落，而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率，会加剧列车横向振动[13]。

 

随着列车速度的增加，隧道内的空气动力学效应显著，导致空气动力学噪声和车体横向晃动的乘坐平稳性降低等问题。因此，研究列车在隧道中运行的空气动力学性能至关重要。choi等[14]通过cfd模拟研究了列车速度、车头长度和堵塞对地铁隧道内列车气动阻力的影响。通过建立比例模型列车研究了雷诺数对隧道内列车表面压力的影响，以说明雷诺数与压力振幅之间的关系。对于在隧道中高速运行的列车，车体周围会产生空气动力，这种力使车体的摆动比在开放路段大得多。说明该空气作用力来自车体下方产生的涡流与隧道壁的干扰，分析认为车体表面与隧道壁面之间空间内存在有组织的流动结构，流场从头车向尾车发展，在尾部分离，导致的周期性的压力波动削弱了列车后部车厢的乘坐平稳性。马伟斌等[19,20]表示列车进入隧道时，隧道内的空气突然产生复杂波动，且会在车体表面形成涡旋，从而严重影响列车运行的安全性、乘坐平稳性以及隧道周边环境，其主要原因是，列车进入隧道尤其是单线隧道，阻塞比大，气动效应明显。早在1986年，日本的新干线上首次观察到列车在隧道中摇摆的现象，其具有以下特征：与明线相比，隧道内列车的摆动幅度更加明显；从列车编组的头车到尾车，摆动逐渐增强；与其它方向上的摆动相比，横向摆动最明显。

 

针对列车在隧道中的晃车现象，国内外已经开展了许多研究。takai等[22]首先证实了隧道内列车晃车现象和轨道不平顺之间没有直接关系，空气动力是主要因素。suzuki等[23]进行了大量的实验和数值分析，表明列车在隧道内运行时，尾涡的旋涡脱落是横向振动加剧和乘坐平稳性下降的原因。diedrichs等[24,25]采用大涡模拟les方法研究了德国ice2高速列车和日本s300新干线列车在隧道中的尾车振动，其中通过les获得的空气动力学载荷直接施加到车体上，他们发现尾车振动与列车尾部头型和车体质量有关。根据在隧道内运行的试验列车车体表面测得的压力数据，建立了空气动力模型。接着他们建立了一个八节编组列车的分析模型，通过在车体上横向施加空气动力，研究了了列车在隧道内高速行驶时的乘坐平稳性。杨吉忠[28]针对大阻塞比双线隧道内列车横向气动性能恶化的现象，利用高速列车空气动力作用模型，对隧道内高速列车周围的流场进行数值计算，详细分析了作用在列车上的气动力和力矩，并针对不同列车形状、隧道结构形式、线间距等因素对气动力特性的影响展开了研究。研究发现尾车的横向振动要比头车和中间车更加剧烈，通过增加列车头型长度或增大隧道截面积，可以有效抑制作用在尾车上的气动力和力矩，有利于减缓尾车横向晃动。

 

最近两年，中车集团对相关列车的晃车问题开展了测试研究。其中，中车长春轨道客车股份有限公司的韩光旭等[29]对某型号高速动车组尾车横向晃动进行了研究，结果表明新轮时轮轨匹配等效锥度偏低，转向架蛇行频率及车辆滚摆频率皆与尾部涡流扰动频率接近，导致尾车发生较大的横向晃动。对时速160公里市域动车组隧道内运行动力学特征进行了测试分析，研究了尾车晃动机理，并结合空气动力学计算结果建立了考虑尾车空气涡流的车辆系统动力学模型，分析了车辆悬挂参数及轨道不平顺对列车尾部横向晃动的影响，对横向减振器阻尼及抗蛇行减振器阻尼进行了优化试验研究，测试结果发现尾车晃动频率与其蛇行运动无关。

 

据作者所知，几乎所有关于高速列车隧道空气动力学的研究都将计算的空气动力学载荷作为外部激励应用于车辆动力学模型，而尚未对车辆的流固耦合振动进行研究。同时，现有的研究更多地关注列车尾部的振动响应，而很少关注隧道内作用在车体上的空气作用力响应。本文围绕动力集中型动车组在隧道内的列尾晃车问题，在传统列车空气动力学和车辆系统动力学分析方法的基础上，构建了隧道尾车流固耦合振动的仿真平台，再现动车组列尾较大幅值的低频晃车现象，根据车辆系统动力学与涡激振动理论系统地研究动车组列尾晃车机理，并通过轨道线路测试对仿真结果进行了验证。

 

2.动力学建模

2.1列车-隧道空气动力学模型

空气动力学仿真采用商用cfd软件simuliaxflow2021x，它使用了基于格子玻尔兹曼方法（lbm）的粒子法。与传统的网格法模拟相比，基于粒子法的xflow的可以更容易的模拟运动部件及流体-结构的相互作用，其自适应尾流细化功能可以动态跟踪流动发展过程中的尾流。其采用大涡模拟（les）进行湍流建模，les湍流模型在很长一段时间内没有被广泛使用，因为与具有navier-stokes解算器的rans模型相比，计算成本相对较高。lbm方案以低计算成本使用les湍流模型。作为一种相对先进的研究方法，les湍流模型擅长于高湍流和分离流的瞬态分析，而rans模型大多局限于稳态分析。近年来，les模型已被有效地应用于模拟全尺寸列车的空气动力学中。

 

用于仿真的动力集中型动车组在单线隧道运行中的空气动力学模型如图1所示，考虑到计算资源和空气动力学计算的准确性，建立了一个6节车和400m长隧道的简化的1:1比例的列车-隧道模型进行研究。其中尾车的长度为4.4h，中间车辆长度为6.38h，每辆车宽度为0.83h。高度h为4.0m，h也被定义为特征长度，即从轨面到列车车顶的高度。

 

此外，根据gb146-2的标准[37]，单线隧道的高度为6.55m，宽度为4.88m。，轮对下表面距离地面高度设置为0.05h，车间的间隙设置为0.1h。计算域和边界条件如图1(d)所示。计算域的总长度为100h，单线隧道入口和出口边界条件分别设置为速度入口和压力出口，其中入口速度u是列车的运行速度，出口压力设置为0。根据en14067-6标准，列车位于入口边界下游20h处，尾流场在x方向上延伸45h。在本文的仿真中，通公式（1）计算的雷诺数为8.09×106。

 

 

 

 

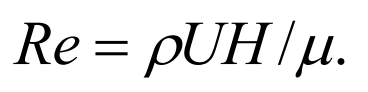
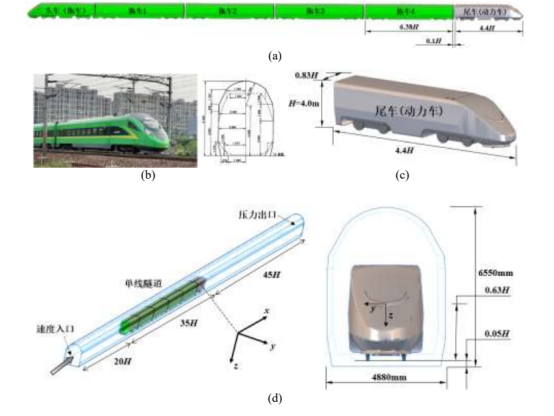
图1.列车隧道的空气动力学模型

 

在本研究中，计算粒子网格是由xflow生成的d3q27组织的八叉树晶格结构。考虑到列车的外型，为了更好地模拟列车尾流的涡流结构，采用了动态尾流细化，并使用了三个细化框，如图2所示。产生了六个级别的八叉树结构，其中远场（level6）中的粒子分辨率为0.064h，尾部车体表面附近和尾流中的精细粒子（level1）的分辨率为0.002h。

 

 

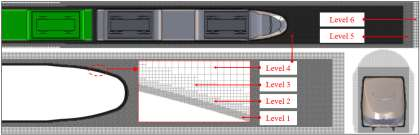
图 2. 计算域网格.

 

2.2 车辆多体动力学模型

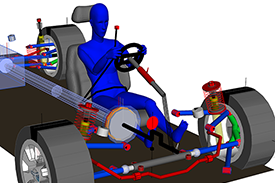
动力集中型动车组的动力车（b0-b0 机车）的动力学模型由商用多体动力学软simulia simpack 2020 建立，如图 4 所示。动力学模型由 25 个刚体组成，包括一个车体、两个转向架构架、两个牵引杆、四个轮对、四个电机、四个空心轴和八个轴箱转臂，一共 90 个自由度。其中，车体、转向架构架、轮对和电机具有六个自由度。每个空心轴有三个自由度，每个牵引杆有两个自由度，而每个转臂只有一个自由度。此外，轨距设置为1435 mm，轮轨法向力由 simpack 中的 fastsim 算法计算。此外，在以下时域模拟中，采用高速轨道谱作为轨道激励。

 

 

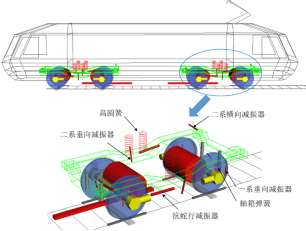
图 3. 列尾动力车的动力学模型

 

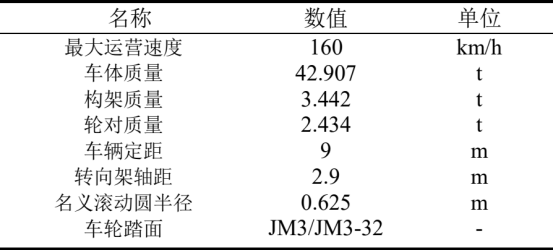
通常，车辆的悬挂系统由一系悬挂和二系悬挂构成。一系悬挂作用于轮对和转向架构架之间，包括转臂、轴箱弹簧和一系垂直减振器。二系悬挂作用于转向架构架和车体之间，由高圆弹簧、二系横向减振器、二系垂直减振器、抗蛇行减振器和二系横向止档组成。此外，还考虑了阻尼器和止挡元件的非线性特性。动力车的结构和悬挂参数如表 1 所示，动力学模型的准确性已在之前的文章[40,41]中得到验证。

 

表 1. 动力车主要参数

 

 

2.3 流固耦合仿真模型

基于上述列车空气动力学模型和车辆动力学模型，对尾车在隧道内的流固耦合振动进行了仿真计算，如图 4 所示。根据 fmu/fmi 标准，采用实时数据动态交换方法模拟了该流固耦合振动。其中坐标系原点（0, 0, 0）为尾部车体的几何中心，其距离轨道表面的高度为 0.63h，如图 4(d)所示。对于该流固耦合过程，车辆动力学模型将车体的三种运动状态传递给列车空气动力学模型，包括横向位移 y、侧滚角 α 和摇头角 γ。然后，列车空气动力学模型将计算出的空气动力学载荷（包括横向力 fy、侧滚力矩 mx 和摇头力矩 mz）实时传递给车辆动力学模型。此外，采用 0.05 ms 的统一时间步长仿真步数共 800×103，以确保瞬态分析中流量的充分发展。

 

 

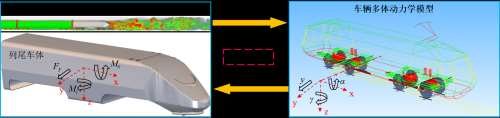
图 4. 列尾流固耦合振动仿真平台.

 

3. 车辆动力学性能指标

3.1 乘坐平稳性

目前，世界各国对铁道车辆乘坐平稳性的评价方法多种多样，如 vdi 2057、us bs 6841、sperling 平稳性指标、iso 2631-1、uic 513、en 12299 等，其中后四种较为常用。本文中，采用 sperling 平稳性指标来评价铁路车辆的平稳性，这里只分析横向平稳性指标wy，其计算公式如下：

 

 

 

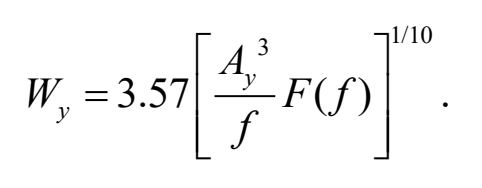
其中 ay 为横向振动加速度幅值，f 为对应频率，f(f)为频率修正系数。可以看出，横向平稳性指标 wy是通过对振动加速度进行统计处理得到的，测量位置一般在车辆地板上。为了研究列尾动力车的横向平稳性，本文对列尾车体的振动加速度进行了测量，得到了相应的横向平稳性指标。此外，wy 值越小，表示横向平稳性越好，机车横向平稳性指标小于2.75 表示优等级。

 

3.2 运行安全性

一般来说，铁道车辆动力学性能的运行安全指标与车辆所受的作用力有关，如轮轴横向力、脱轨系数、轮重减载率和倾覆系数，后三者适用于曲线和侧风工况。本文分析了列车在直线上的横向动力学性能，因此选择轮对横向力来评估车辆的运行安全性。轮对横向力 гwf 为同一轮对上左、右轮轨横向力的代数和，其值过大则会导致轨距加宽或轨道严重变形。根据 gb/t5599[42]标准对轮对横向力的评价如下：

 

 

 

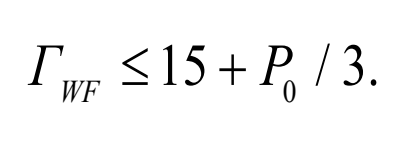
其中 p0为静态轴重，单位 kn，本文研究的动车 p0约为 189 k n，计算得到的轮对横向力 гwf限值为 78 kn。

 

4. 仿真结果分析

4.1 仿真工况

本节根据列车的实际运行工况，设置三种计算工况，分别对应三种不同的车轮踏面，具体如下：

 

cond 1：jm3_new，等效锥度为 0.1；

cond 2：jm3_worn，等效锥度为 0.4；

cond 3：jm3-32 薄轮缘，等效锥度为 0.04。

 

此外，列车的运行速度设置为 130 km/h，轨底坡设置为 1/40。在此基础上，分别对三种等效锥度下的单线隧道内列尾动力车的车辆动力学性能和气动力响应进行了分析。

 

4.2 车辆动力学性能响应

为了研究流固耦合对车辆动力学性能的影响，表 2 显示了有气动载荷和无气动载荷时的动力学性能结果。可以看出，气动力对隧道内列尾动力车的动力学性能的影响主要体现在其横向平稳性上。在不考虑气动载荷的情况下，随着等效锥度的减小，车体后端的横向平顺性指数 wy 减小，即车体摇摆加剧，但仍处于优级别。当施加气动力时，车体后端的wy在 cond 1 和 cond 3 下超过 2.75 的极限值，这将导致列尾剧烈振动。然而，气动载荷对动力车辆的运行安全性（轮对横向力）几乎没有影响。列车尾部附近四位轮对的轮对横向力在空气动力载荷作用下虽然相对较大，但远小于其极限值 78 kn。

 

表 2. 车辆动力性能响应（无/有气动荷载作用）.

 

 

接着对 jm3 新轮型面 cond 1 下的列尾车体横向振动加速度进行分析，其时域和频域结果如图 5 所示。从图 5(a, c)可以看出，隧道内的气动效应主要加剧了车体后部的横向振动加速度，而对车体前端的横向振动加速度几乎没有影响。如图 5(b, d)所示，在没有气动载荷的情况下，车体横向振动的主频为 1.3 hz，即车辆蛇行频率。此外，在气动载荷作用下，车体横向振动加速度响应仍以车辆蛇行频率 1.3 hz 为主。在车体横向振动剧烈的轨道区段，流固耦合效应会更加明显，对应图 5(c)中的蓝色方框标记。

 

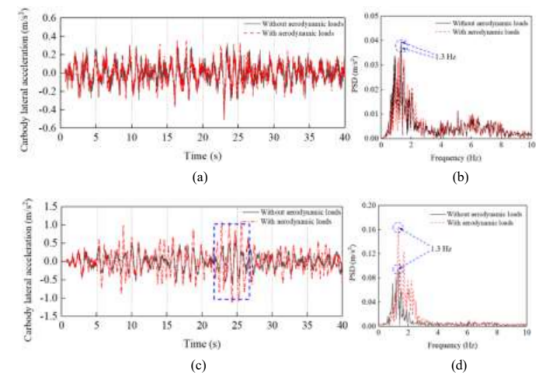
图 5. cond 3 下车体横向振动加速度.

 

4.3 列尾气动力响应

在三种类型的轮轨接触条件和车体固定的独立的流体仿真中，作用在尾部车体上的空气动力学载荷的振幅如表 3 所示。可以看出，在 130 km/h 的速度下，气动横向力 fy的幅值约为 4.5–6.0 kn，摇头力矩 mz的幅值约为 35–60 kn·m，侧滚力矩mx的幅值约为 1.5–2.5 kn·m。

 

表 3. 不同轮轨等效锥度下的气动载荷.

 

 

然后，对高锥度 cond 2 和低锥度 cond 3 下的列尾气动力响应进行了对比分析。如图7(a, c, e)所示，作用在列尾车体上的气动载荷随时间近似正弦变化。同时，随着等效锥度的减小，车体振动加剧，作用在车体上的气动载荷幅值增大，这意味着流固耦合效应增强。从图 7(b, d, f)中可以看出，随着车体晃车的加剧，作用在列尾的气动载荷频率，也称为涡流脱落频率，从 1.7 hz 变为车辆蛇行频率 1.3hz，表明发生了涡激共振（viv）的锁频现象，流固耦合效应改变了旋涡脱落频率并引起了结构共振。

 

 

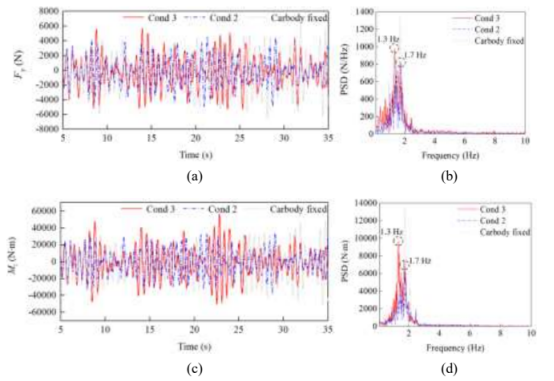
图 6. cond 3 和 cond 2 下的列尾气动力.

 

5. 线路试验

5.1 测试线路

试验线路为中国云南玉溪至蒙自铁路，具有隧道线路占比大的特点。玉溪至蒙自铁路于 2019 年正式通车，全长 150 公里。其中，隧道 35 座，桥梁 61 座，占线路总长的55 %。科研团队于 2022 年 11 月对该动力集中动车组的 8 辆短编组（1 辆动力车 7 辆控制车）列车进行了跟车线路试验，并对列尾动力车的动力学性能进行了分析。

 

 

(a) (b)

图 7. 测量目标.

 

轮轨接触状态对铁路车辆动力学具有重要意义，影响铁路车辆的乘坐平稳性和运行稳定性。如图 7(a)所示，对 jm3 新车轮踏面和行驶 6.9 万公里后的磨耗轮踏面进行了测量。此外，两个车体振动加速度传感器分别安装在车体地板表面。如图 7(b)所示，一个安装在动力车后端的驾驶室中，另一个安装于动力车前端的设备间中。为了准确分析车辆的乘坐平稳性，加速度传感器的采样频率设置为 1000 hz，范围为 2 g（g 为重力加速度，其值为9.8 m/s2）。

 

5.2 车轮踏面测量

如图 8 所示，车轮踏面的主要磨损区域集中在名义滚动圆周围的-20～30 mm 范围内。在轮缘厚度保持不变的情况下，磨耗轮在运行 69,000 km 后的最大磨耗深度为 0.58 mm。然后，计算了标准 uic60 钢轨下轮轨接触横向位移 3 mm 处的匹配等效锥度 λ，其中在 jm3新车轮型面下等效锥度 λ 约为 0.10，而在 jm3 磨耗车轮型面下的等效锥度 λ 增大到 0.40。

 

 

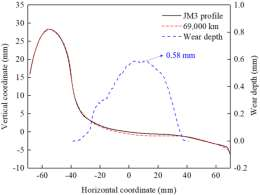
图 8. 车轮轮廓和车轮踏面的磨损深度.

 

5.3 车体振动加速度

取线路上典型的隧道工况如图 9 所示，由两个隧道和一座连接桥组成。由于隧道内信号不佳，我们根据司机的行车记录仪大致记录了列车的运行速度。曲线隧道运行速度约为117 km/h，直线隧道限速段运行速度约 60 km/h，其他单线直线隧道运行速度为 120～130 km/h。隧道工况下列尾后端驾驶室的横向平稳性指标 wy如图 9(a)所示，其中未标记的路段为单线直行隧道。可以看出，在曲线隧道运行过程中，由于此时轮缘和钢轨贴合，车体振动不剧烈，因此横向平稳性较好。在双线隧道和限速直道隧道中运行时，气动效应不明显，横向平稳性很好。然而，在单线直道隧道工况下，当速度增加到 120–130 km/h 时，wy的值立即增加到 2.75 以上，横向乘坐平稳性将迅速恶化。此外，如图 9(a)所示，jm3 新车轮下的横向乘坐平稳性比磨损车轮下的要好得多，新轮和磨耗轮下后司机室的横向平稳性指标 wy的峰值分别为 3.2 和 3.0。

 

 

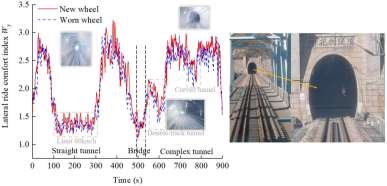
图 9. 隧道工况平稳性.

 

隧道运行中后司机室的横向振动加速度如图 10 所示。如图 10(a, c)所示，当在单线隧道直线路段运行时，新轮下车体的横向振动加速度明显高于磨耗轮下车体的横向振动加速度。新轮下车体横向加速度幅值达到 0.15 g，磨耗轮下车体横向加速度幅值为 0.12 g。相应的时频结果如图 10(a, c)所示，可以看出，由于列车运行速度在不同路段的变化，后驾驶室的振动能量主要分布在 1–1.5 hz 的范围内。此外，在 380 s 左右乘坐平稳性最差的单线隧道条件下，列车尾部晃车频率主频为车辆蛇行频率的 1.3 hz。

 

 

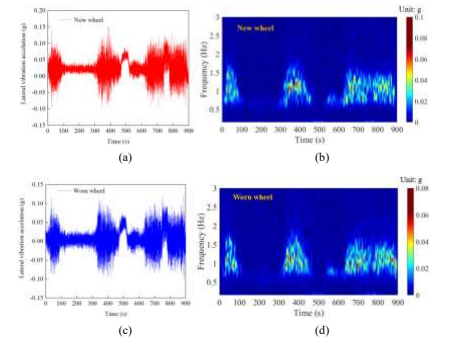
图10.隧道工况列尾车体的横向加速度.

 

综上所述，动力集中动车组在明线上的运行平稳性表现良好，但在单线隧道工况下，列车尾部的横向平稳性显著下降，这是由尾涡的气动效应引起的。然而，列车尾部车体的横向振动是否与尾流中旋涡脱落导致的强迫振动有关，该涡脱落频率为多少？根据仿真和试验结果，在 130 km/h 速度下，旋涡脱落频率为 1.7 hz，接近车辆蛇行运动频率 1.3 hz，导致了涡激振动的发生。随着车体晃动的增大，流固耦合效应会增强。流固耦合作用改变了旋涡脱落频率，引起结构共振，进一步恶化了车体的乘坐平稳性，晃车频率由车辆蛇行频率主导。

 

6. 结论

本文针对动力集中型动车组列尾动力车在单线隧道内的晃车现象，进行了不同轮轨接触等效锥度下的空气动力学与车辆系统动力学耦合仿真及线路试验研究，结果如下：

 

(1) 仿真再现了单线隧道内列尾动力车的横向持续晃车现象，表明作用在列尾车体上的气动力是导致晃车的主要因素。同时晃车的主频与车辆蛇行频率一致，在轮轨接触等效锥度较低的工况下车体横向晃动会更加剧烈。

 

(2) 在独立的流体仿真中，车速为 130 km/h 时，列车尾流的旋涡脱落频率为 1.7 hz，即气动载荷和车体横向振动加速度的频率为 1.7 hz。然而，在线路试验和流固耦合仿真中列尾晃车的主频变为车辆蛇行频率 1.3 hz。这表明发生了涡激振动（viv）引起了锁频现象，流固耦合作用改变了旋涡脱落频率从而引起结构共振，因此单线隧道内列尾持续晃车问题需要进行流固耦合分析。

 

(3) 从本文的研究角度，减小流固耦合效应有利于改善单线隧道中列尾的持续晃车现象。例如，提高车体的蛇行稳定性，以及通过改善悬挂参数来降低车体尾部的振动幅值等都是行之有效的措施，这些措施在实践中得到了验证。